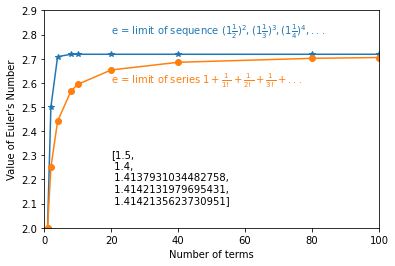
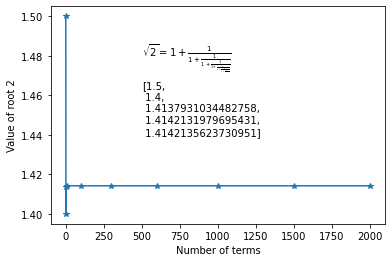
Einstein called this "the most interesting book on the evolution of mathematics which has ever fallen into my hands."
Number was first published in 1930 with the fourth edition coming out in 1954. This is a republication of that fourth edition (Dantzig died in 1956) edited by Joseph Mazur with a foreword by Barry Mazur. It is an eminently readable book like something from the pages of that fascinating four-volume work The World of Mathematics (1956) edited by James R. Newman in that it is aimed at mathematicians and the educated lay public alike.
Part history, part mathematics and part philosophy, Number is the story of how we humans got from "one, two...many" to various levels of infinity. Strange to say it is also about reality. Here is Dantzig's concluding statement from page 341 in Appendix D: "...modern science differs from its classical predecessor: it has recognized the anthropomorphic origin and nature of human knowledge. Be it determinism or rationality, empiricism or the mathematical method, it has recognized that man is the measure of all things, and that there is no other measure."
Or more pointedly from a couple of pages earlier: "Man's confident belief in the absolute validity of the two methods [mathematics and experiment] has been found to be of an anthropomorphic origin; both have been found to rest on articles of faith."
These are inescapably the statements of a postmodernist. I was surprised to read them in a book on the theory of numbers, and even more surprised to realize that if mathematics is a distinctly human language, it is entirely possible that beings from distant worlds may speak an entirely different language; and therefore our attempts to use what many consider the "universal" language of mathematics to communicate with them may be in vain.
And this thought makes me wonder. Is the concept "two," for example, (as opposed to the number "2") really just a human construction? Would not intelligent life anywhere be able to make a distinction, just as we have, between, say, two things and three things? And if so, would they not be able to count? And would not then the entire edifice of mathematics (or at least most of it) follow?
I wonder if Dantzig was not in contradiction with himself on this point because earlier he writes (p. 252) "...any measuring device, however simple and natural it may appear to us, implies the whole apparatus of the arithmetic of real numbers: behind any scientific instrument there is the master-instrument, arithmetic, without which the special device can neither be used nor even conceived." Does this not imply that measurements (by any beings) and therefore numbers have an existence outside of the human mind and do not rest on "articles of faith"?
As to the numbers themselves (putting philosophy aside) we learn that the two biggest bugaboos in the history of number are zero and infinity. It took a long, long time for humans, as Dantzig relates, to accept the idea of zero as a number. Today zero is also a place-holder. But what does it mean to say that there are zero pink elephants dancing about my living room? I can see one cow in the yard, or two or three, but I cannot see zero cows in the yard.
Of course, today it is easy to see that zero is a number that is less than one and greater than minus one. I have one cow and I sell that one cow. Now I have zero cows. (Curiously, note that the plural noun "cows" is grammatically required.) However, the imperfect fit within the entire structure of mathematics that zero has achieved may be appreciated by realizing that every other number can be a denominator; that is, three over one equals three, three over two equals 1.5, etc., but what does three over zero equal?
It is a convention of mathematics to say that division by zero is "undefined." There is no other number about which the same can be said.
I used to think when I was young that infinity was the proper answer to division by zero. For Dantzig this is clearly not correct because to him infinity is not a number at all but a part of the process. He writes, "the concept of infinity has been woven into the very fabric of our generalized number concept." He adds, "The domain of natural numbers rested on the assumption that the operation of adding one can be repeated indefinitely, and it was expressly stipulated that never shall the ultra-ultimate step of this process be itself regarded as a number." Of course he is talking about "natural" numbers. He notes in the next sentence that in the generalization to "real" numbers, "the limits of these processes" were "admitted...as bona fide numbers." (p. 245) In other words, part of the process became a number itself!
The culmination of Dantzig's argument here is that infinity itself is a construction of the human mind and exists nowhere (that we can prove) outside of the human mind. He believes that the basis for our belief in the existence of infinity comes from our (erroneous) conception of time as a continuum. Dantzig notes that Planck time and indeed all aspects of the world are to be seen in terms of discrete quanta and not continuous streams.
Ultimately, Dantzig gives this sweeping advice to the scientist: "...he will be wise to wonder what role his mind has played in...[a] discovery, and whether the beautiful image he sees in the pool of eternity reveals the nature of this eternity, or is but a reflection of his own mind." (p. 242)
--Dennis Littrell, author of “The World Is Not as We Think It Is”